پیدا کردن ضابطهای جبری برای اعداد اول جزو یکی از معماهای ریاضی باقیمانده بود تا اینکه درست در اردیبهشت ماه 1386 سید محمدرضا هاشمی موسوی فرمولی از اعداد اول کشف کرده که دانشمندان برای حل این مساله و دریافت جایزه یک میلیون دلاری آن تا سال 3001 فرصت داشتند که پرفسور هاشمی موسوی فرمول این اعداد را برای اولین بار کشف و به نام خود ثبت کرد. پرفسور هاشمی موسوی، دکترای ریاضی از دانشگاه بوستون کتابی نیز در این زمینه چاپ کرده است که امید می رود جایزه ای را در ریاضیات به خود اختصاص دهد.
تاکنون بیشترین توفیق ریاضیدانان در این زمینه به سه جمله ای اویلرf(x) = x2 + x + 41 باز می گشت که به ازای عددهای درست پشت سر هم از x = 0 تا x =39 همواره برابر با عددی اول می شد اما در این تابع f(40) = 412 ، عددی مرکب است. اعداد فرما هم که به ازای اعداد ۰ تا ۴ اول می شدند. ولی فرمول پرفسور هاشمی موسوی به ازای تمامی اعداد اول است و تمامی اعداد اول را نیز تولید می کند!
پروفسور سید محمدرضا هاشمی موسوی کاشف فورمول اعداد اول (blogfa.co
در سایتی دیگر میخوانیم:
فرمول اعداد اول توسط پرفسور سيد محمد رضا هاشمي موسوي کشف شد
بالاترین: فرمول اعداد اول توسط پرفسور سيد محمد رضا هاشمي موسوي کشف شد (balatarin.com)
در سایت دبیرستان علامه جعفری چنین نوشته:
كشف فرمول اعداد اول توسط سید محمد رضا هاشمی موسوی
آيا تا به حال درباره فرمولي كه اعداد اول را توليد كند فكر كرده ايد.افراد زيادي در به دست آورن اين فرمول كوشيده اند.اما نتيجه ای نگرفته اند.ادعا شده است كه فرمولی كه در زير آورده شده است اعداد اول را توليد مي كند.
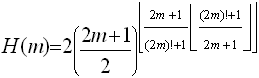
كشف فرمول اعداد اول توسط سید محمد رضا هاشمی موسوی (blogfa.com)
یا در سایت digikala.com چنین در مورد کتاب پر فروش و ارزشمند توان و رادیکال نوشته شده:
اینها تنها چند مورد از هزاران سایتی هستند که به انگلیسی و فارسی در مورد کشف بزرگ فرمول اعداد اول و نتایج آن نوشتند.

